投资组合分析投资组合收益和风险的计算公式

投资组合分析,二战结束后，美，欧经济发达，股市回暖，人们的投资需求逐渐增加。投资的本质是在权益和风险之间进行选择，因此对与风险和收益如何度量，如何平衡这两个指标，是投资者需要解决的关键问题。想要了解更多相关消息可以看一下股票投资规律.

在这样的背景下，52年马科维茨发表的论文《资产组合的选择-投资的有效分散化》，代表着现代投资组合理论(MPT)的正式诞生。这个理论主要包括均值方差分析方法和投资组合有效边界模型，并且在实际的应用中得到了证明，被看作近代金融的开端，还因此获得了90年的诺贝尔经济学奖

均值方差分析方法,投资是一种节省当前消费并期望未来有更高消费能力的行为。收益是未来消费能力的较高部分，风险代表获取收益的不确定性。投资时要考虑的前两个因素是利润和风险。未来收益是不确定的，是随机变量，所以不可能用一个确定的值来描述收益率。随机变量一般用概率分布来描述。概率分布的两个重要数值特征是均值和方差

均值方差分析法在描述收益率时使用了概率分布的均值，由于均值也称为数学期望，所以这种描述称为期望收益率，记录为E(R)。在描述风险时，使用概率分布的方差并记录为风险值。方差表示分布的离散度，离散度可以描述不确定性。根据概率分布的知识，var (e)=e {r-e (r)} 2

投资组合有效边界模型如果你做多项投资，你会得到一个投资组合。那么如何根据单笔投资做出最佳组合呢?投资组合与每笔投资的回报和风险有什么关系?根据以前的平均方差分析方法，我们可以把问题转化为研究联合分布和单分布的关系。通过研究得到了马科维茨投资组合的有效边界模型。

马科维茨观察了不同投资的组合，推导出不同权重下各投资的风险收益曲线，即联合分布的方差(标准差)-均值曲线。最后，他发现存在最优投资组合曲线。对于给定的收益率(均值)，这条曲线线上投资组合的风险最小，这条曲线是有效边界，也称为有效前沿。

这个过程需要很强的计算能力，因为在计算一个投资组合的方差时，它是根据个人投资权重和方差投资协会间的联系来求和的。线上的每个点都需要这个计算。例如，如果有一个投资组合有n个投资，那么就有n(n-1)/2个co-要计算，计算量和投资数量是平方的。这个平均值和方差的计算过程可以用下面的公式来描述：

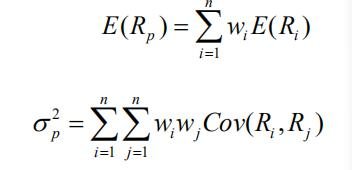
投资组合.jpg